下次要是面试官还拷打我红黑树的实现,我就要掏出这个了!!!
该来的还是来了,面试被拷打后,我连夜把红黑树
看了个精光
本文默认读者已有AVL等平衡树的基础知识,有了平衡树知识红黑树还是很好掌握的,袪魅袪魅
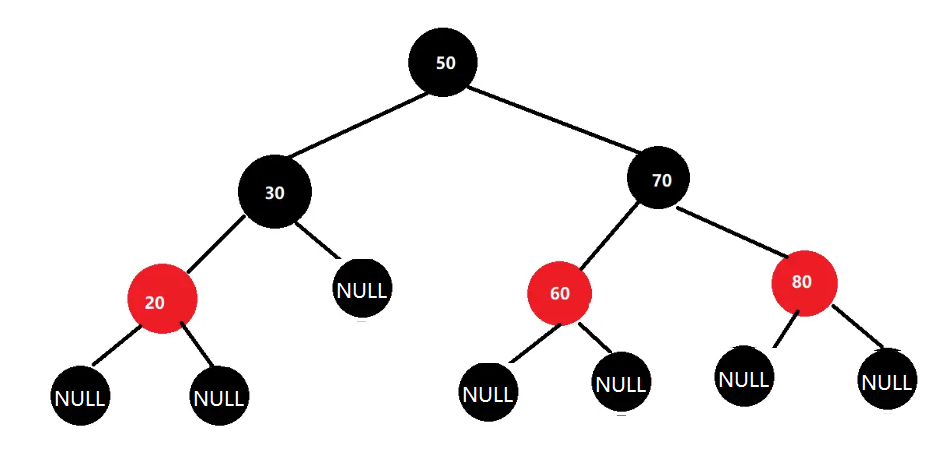
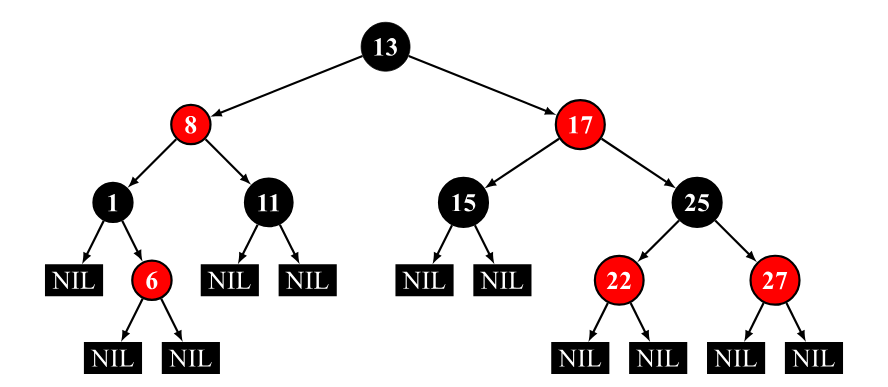
下图是一棵普通的红黑树:
一、红黑树的性质
- 叶子结点都是空结点(null),定义为黑色
- 任意叶子结点到公共祖先的路径上黑色结点数量必须相同(红黑树的平衡定义)
- 叶子到根的黑色结点数也称作:黑高
- 该性质保证任意叶子到祖先路径上的黑点数不超过logn+1
- 红色结点的儿子和父亲必须是黑色
- 保证任意2条叶子到根的路径,长度差不超过黑高的2倍
- 复杂度的保证:任意叶子到根的距离不超过2logn+1
- 只有红色或黑色结点
- 根必须是黑色(单纯为了方便维护)
对红黑树的旋转/颜色变更,实际就是保证被操作的每棵子树,操作结束后都是要维持性质2,3成立
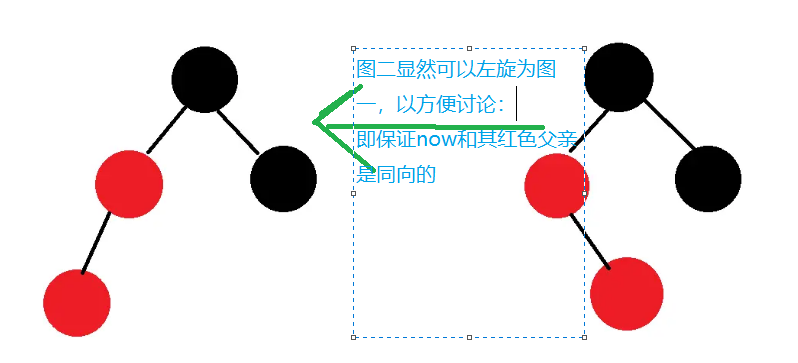
下文对红黑树的讨论都是基于结点为左儿子(右儿子处理方法同理)
下文定义结点的方向是否同向:即都为各自父亲的左儿子(或都是各自父亲的右儿子)则同向,否则不同
二、查询和旋转操作
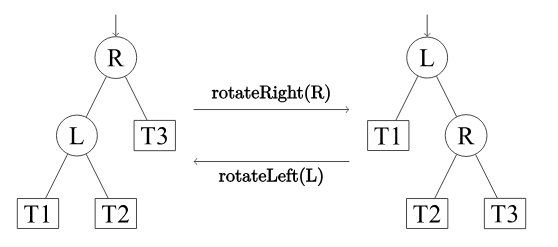
红黑树也是平衡树,他的查询和旋转操作和一般平衡树没什么区别,这里强调下左旋和右旋的区别即可。
左旋即是根旋转为左儿子,右旋即是根旋转为右儿子
三、插入操作(双红修正)
1. 插入结点的颜色
- 为了维护性质2黑高不变,我们插入的值初始为红色更为方便维护
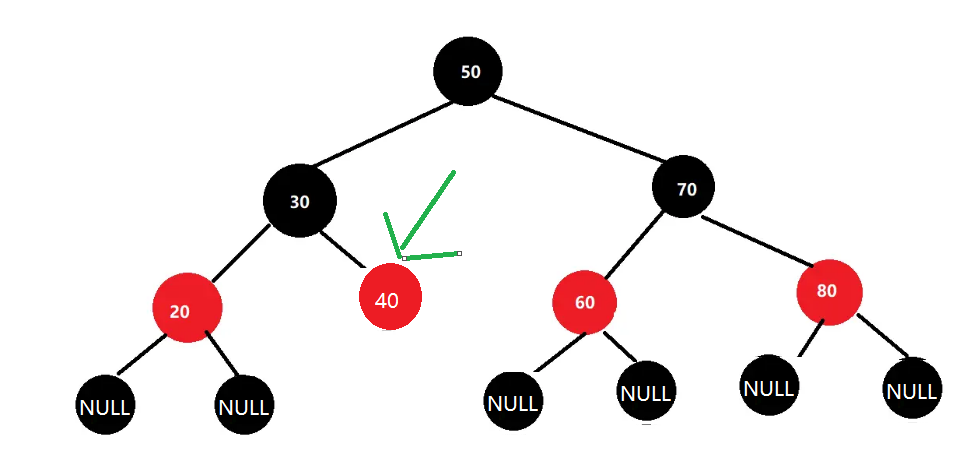
- 一个结点插入成功(不存在这个key),他肯定是把原来的null叶子变成新结点,比如我们上图插入新结点40
2.成功插入后可能存在的问题,如何进行修正?(双红修正)
问题: 插入结点与其父亲均为红色(不满足性质3),修正情况如下
- 定义:双红父子中的儿子为当前结点now(初始为插入结点),父亲为f,祖父为rf
- now的祖父不存在,即父亲为根
- 根据性质5,将父亲直接改为黑色即可,修正结束
- now的祖父存在(显然必须为黑色,因为now的父亲是红色)
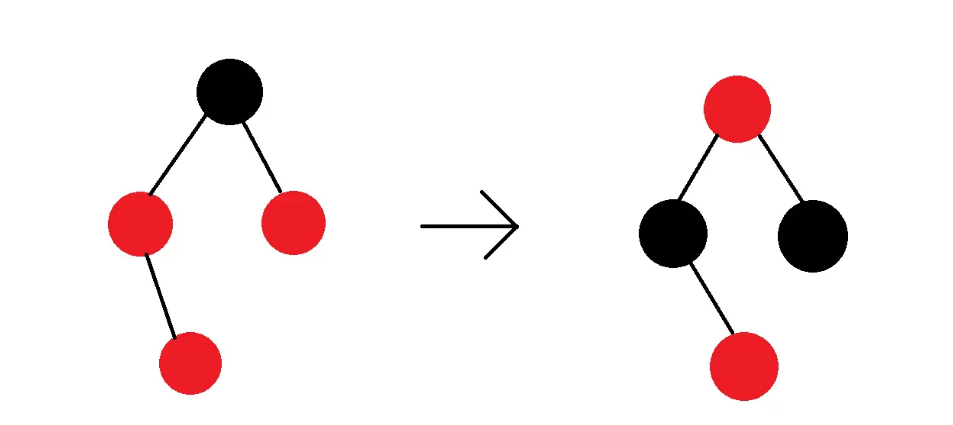
- 情况一:祖父节点的另一子节点也是红节点
- 将now的父亲和叔叔设为黑色,祖父设为红色,now设为祖父,递归考虑新now是否存在双红问题
- 将now的父亲和叔叔设为黑色,祖父设为红色,now设为祖父,递归考虑新now是否存在双红问题
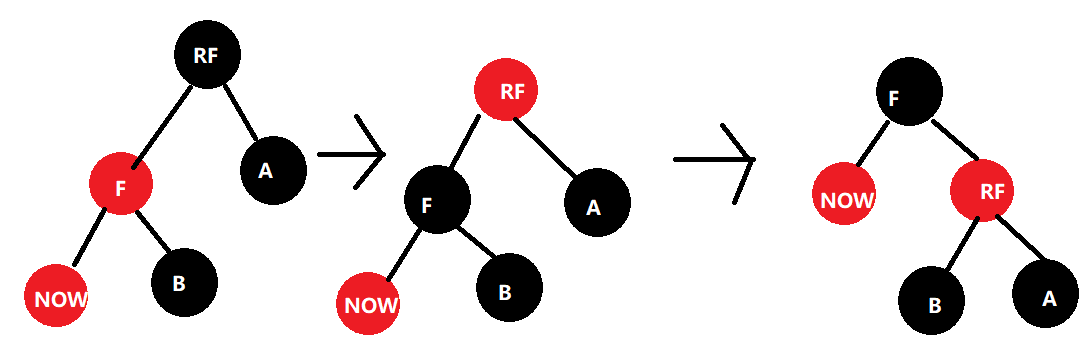
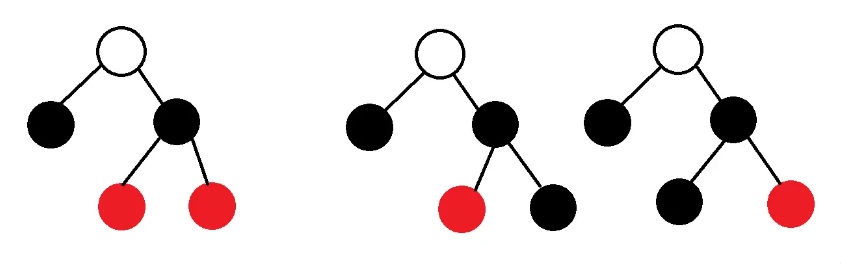
- 情况二:祖父节点的另一子节点是黑节点,存在下图2种情况
- 处理方式如下:f改为黑色,rf改为红色,右旋rf:这样黑高没有改变,双红问题解决,修正结束
- 处理方式如下:f改为黑色,rf改为红色,右旋rf:这样黑高没有改变,双红问题解决,修正结束
- 情况一:祖父节点的另一子节点也是红节点
四、删除操作(双黑修正)
1. 如何删除
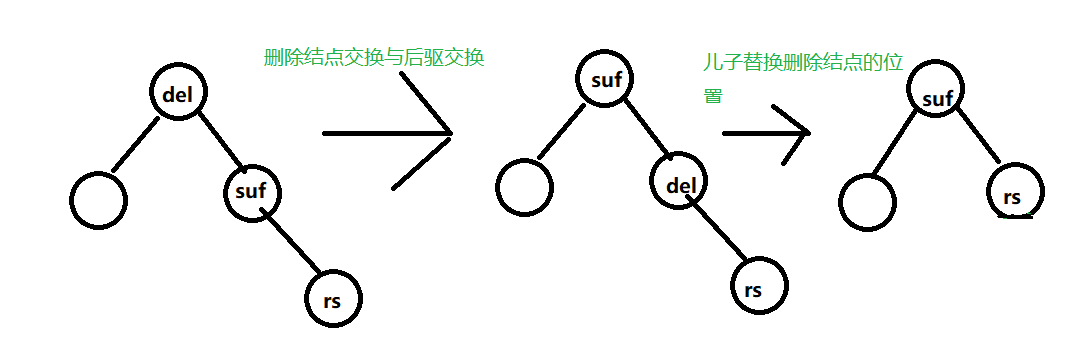
- 删除结点有2个儿子,考虑删除其前驱/后驱(显然其前驱/后驱至多只有一个儿子,本文考虑删除后驱suf),然后把前驱/后驱的值替换到原本打算删除的结点
- 所以我们最终删除的结点至多只有一个孩子
- 如果删除结点有儿子,儿子替换删除结点的位置
- 如果删除结点有儿子,儿子替换删除结点的位置
2. 删除后可能存在的问题,如何进行修正?(不平衡修正)
删除的结点为红色,则没有影响 问题:删除的结点为黑色,则删除结点对应的子树的叶子黑高-1(不满足性质2),修正情况如下
- 定义:标记删除结点的位置为now(如果删除结点有儿子,则儿子的位置为now)
- now的子树黑高平衡,但是now的父亲的子树不平衡,分情况处理父亲的子树不平衡问题:
- 白色结点表示其什么颜色均可
- 如果now是红色结点,或者now是根(不存在父子树),设置now为黑色,修正结束
- now的兄弟bro是黑色
- 且bro的儿子均为黑色
- 将bro改为红色(使其黑高减一),父亲的子树平衡
- 如果父亲为红色,设父亲为黑色,修正结束
- 否则,now设为父亲,递归处理新now的不平衡问题
- 将bro改为红色(使其黑高减一),父亲的子树平衡
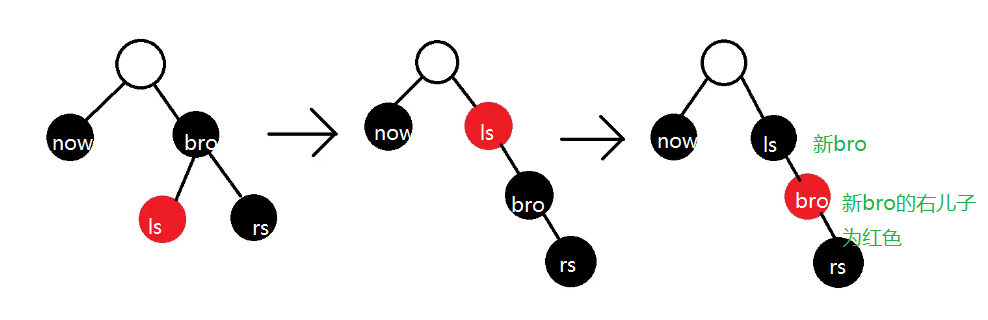
- bro存在一个儿子为红色
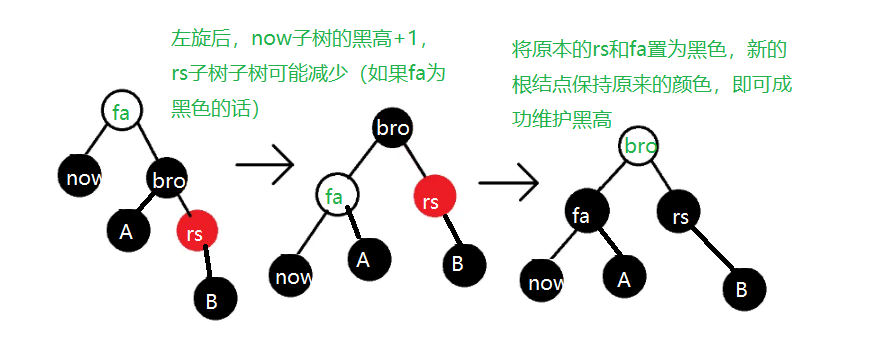
- 如果存在上图情况2,我们先把情况2右旋,并更换新的右子树根和其右儿子的颜色,保证新的bro的与now方向相反的儿子的颜色为红色
- 接下来执行一次左旋,再把第二层的颜色染黑,新根结点颜色保持原来根节点颜色不变即可,黑高问题解决,修正结束
- 如果存在上图情况2,我们先把情况2右旋,并更换新的右子树根和其右儿子的颜色,保证新的bro的与now方向相反的儿子的颜色为红色
- 且bro的儿子均为黑色
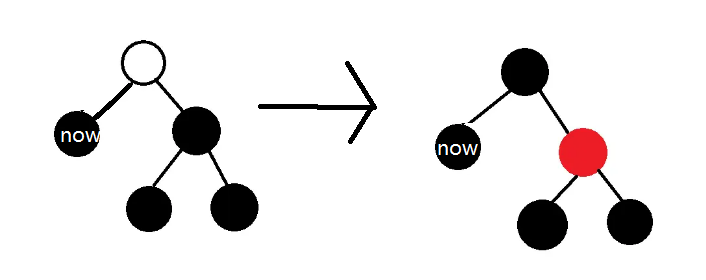
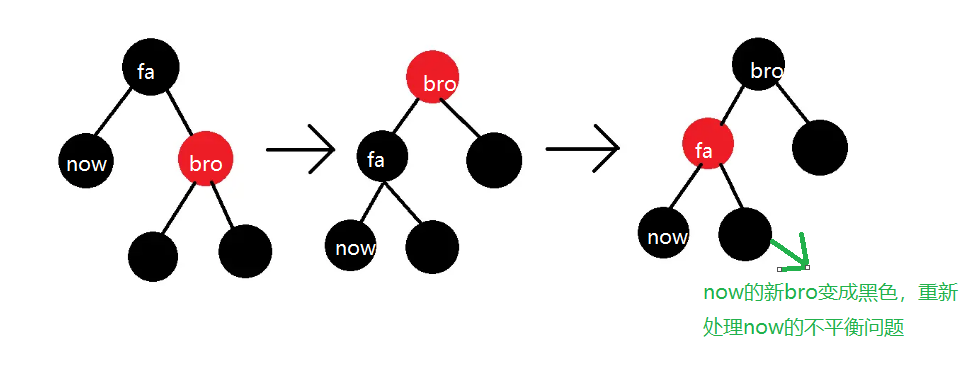
- now的兄弟bro是红色(显然他的儿子必须都是黑色)
- 先左旋,再更换新根和新左儿子的颜色,重新处理now结点
- 这个操作在不改变子树黑高(左子树黑高少1)的同时,now的新bro成为了黑色,使用上面的方案即可解决问题
- 新bro的儿子都为黑色,执行上述方案2.1,递归结束(因为now的父亲变成红色)
- 新bro的儿子有红色,执行上述方案2.2,递归结束
- 先左旋,再更换新根和新左儿子的颜色,重新处理now结点
五、总结:红黑树为何如此优秀
- 虽然红黑树最劣树高为2logn,但是他不平衡的恢复速度极快,这是AVL不具备的!
- 对于插入操作:颜色最多变换O(logn)次,而结束双红修正的旋转操作次数不超过2次
- 对于删除操作,颜色最多变化O(logn)次,而结束不平衡修正的旋转操作次数不超过3次